Maksim Sipos

My research is seemingly in different fields: microbial ecology and fluid dynamics. The unifying feature is that the phenomena in both of these fields are emergent in their nature. In other words, the behaviour of the system in its whole comes about from the collective behaviour of its parts. The basic question that I ask is: how do interactions in these systems lead to global, macroscopic behaviour of the system? My interest is in answering this question in the context of quantitative biology and microbial ecology, as well as in fluid dynamics.

Microbial Ecology

My study of microbial ecology began with my interest in the forces that structure communities of microbes, such as those inhabiting the gastrointestinal tract or waters in the oceans. Because culturing the bacteria is essentially impossible in such cases, for many reasons, research focuses on sampling cellular DNA/RNA from these communities, using techniques known as metagenomics. In metagenomic studies, one sequences the living matter within an environment in order to ascertain the composition of the microbiome, the community formed by the microbes living within that environment. One can observe interesting patterns in metagenomic datasets, such as functional forms of the species abundance curves and the extent of their diversity.

The questions one naturally asks are: what species are present? In what abundance? And how does this community drive the function and evolution of the ecosystem? In the case of microbes, these questions are hard to answer because the species concept is not strictly applicable, and one has to resort to genomics to identify, classify and count the organisms.

In order to be able to study these patterns, I developed a bioinformatics pipeline to process microbial metagenomics datasets [1]. While developing this pipeline, I addressed the problem of multiply aligning large metagenomic 16S rRNA datasets in such a way that analysis artifacts are kept at a minimum. Secondary structure is important for RNA sequences, and hence one should use a secondary-structure aware aligner for regions with strong secondary structure. For regions with no secondary structure (hyper-variable regions), template based aligners are appropriate. I showed that the procedure of combining the two alignment methods using our pipeline outperforms each tool used separately.

To correctly study the ecology of a microbiome using 16S rRNA sequencing, it is also neccessary to be able to cluster the sequenced 16S tags into OTUs (Operational Taxonomic Units). I developed a clustering tool that can perform a good clustering procedure in a way that minimizes the artifacts due to overlapping clusters. The clustering algorithm is also sufficiently fast so that it is applicable to contemporary large datasets.

With the appropariate bioinformatics tools developed, I turned my attention to the problem of understanding the diversity, composition and ecological community structure of the gastrointestinal microbiomes. The perspective that I acquired is a physical one: the OTUs are considered as points in a high-dimensional sequence space as illustrated below.

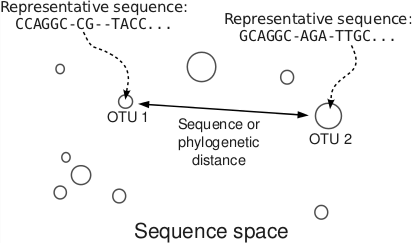
With this view of a metagenomic dataset, the next question was: how do microbial communities assemble? When carrying capacity for an additional bacterium is available, where does this additional bacterium come from? Does it enter the community through a cell division, or immigration? I implemented fast large dataset dimensional reduction methods such as PCA and NMDS, as well as physical models and digital life simulations to study this problem. As a result, I have formulated a novel metric that quantifies the degree by which interactions underlie the assembly of a microbial ecosystem [2].

I applied this metric to 16S metagenomic studies of 6 vertebrate gastrointestinal microbiomes and found that they assembled through a highly non-neutral process. This is despite the fact that OTU abundance curves in these datasets perfectly match the results of Hubbell’s Neutral Theory. This indicates that abundance approaches alone are not sufficient in studying microbial communities; an approach that combines abundance and genomic data is necessary.

Transition to Turbulence

In fluid dynamics, my research has focused on the study of the transition to turbulence. The phase of the flow depends upon the Reynolds number, Re, the dimensionless ratio of the force driving the flow to viscous dissipation. In pipe flows, even at high Re, laminar flow is possible but the slightest disturbance nucleates the state of turbulence. The regions of turbulence (turbulent “slugs”) can expand but they can also spontaneously decay back to laminar flow (turbulent “puffs”). In physics, the abstract process of directed percolation has these same properties: sites on a lattice that are active can expand or spontaneously become inactive (absorbed).

Directed percolation is a ubiquitous process in nature: it occurs in a wide range of problems such as fluid percolation through porous rock, species expansion in ecology and spread of infections and immunity. Can the transition to turbulence problem be in the directed percolation universality class? Yves Pomeau had this intution in 1986 and I set out to quantitatively test its validity [3]. The analogy between transition-to-turbulence and directed percolation is illustrated in the figure below where the phase diagram of pipe flow (as function of Re) is compared to the phase diagram of directed percolation (as function of percolation probability p).

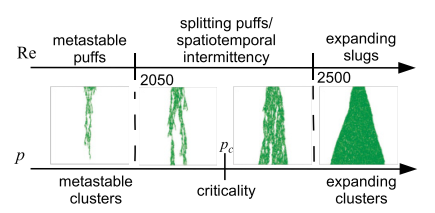
I simulated the directed percolation process in 3+1 dimensions in a pipe geometry (3D videos of the simulations are available here). Under the critical threshold, I found that the characteristic lifetimes of the active states are superexponential in p. The same functional form for lifetimes of puffs in pipe flow experiments has been observed experimentally. Also, the front growth rates of active regions in supercritical directed percolation match those observed in turbulent slug experiments. Without using any details of Navier-Stokes equation of fluid flow, I find that Directed Percolation model fits the experimental data.

Although Pomeau gave intuitive arguments to support this conjecture, it is important to be able to show in more detail how the mapping between Navier-Stokes turbulence and directed percolation might arise. I considered the transition to turbulence in Burgers’ Equation. Burgers’ equation is a simplified form of Navier-Stokes equation, with the pressure term dropped. The pressure term is important for creation of vorticity in turbulence. However, we’ve found evidence that under the directed percolation transition scaling the pressure is an irrelevant variable. The Burgers’ equation has a mapping to the directed polymers model, and there is a directed percolation transition in the directed polymers model.

Taken together, this quantitative evidence suggests that the transition to turbulence occurs as a statistical phenomenon, a non-equilibrium phase transition in the directed percolation universality class. The details of Navier-Stokes equations governing the flow are not neccessary to explain the observed puff lifetimes and turbulent front growth rates in pipe flow experiments. More generally, the transition to turbulence in any fluid described by Navier-Stokes equation may be in the Directed Percolation universality class.

Selected Publications

1. M. Sipos, P. Jeraldo, N. Chia, A Qu, A. S. Dhillon, M. E. Konkel, K. E. Nelson, B. A. White and N. Goldenfeld. Robust computational analysis of rRNA hypervariable tag datasets. PLoS ONE 5, Issue 12, e15220 (2010).
2. P. Jeraldo* , M. Sipos* , N. Chia, J.M. Brulc, A.S. Dhillon, M.E. Konkel, C.L. Larson, K.E. Nelson, A. Qu, L.B. Schook, F. Yang, N. Goldenfeld, and B.A. White, Quantifying the Role of Neutral and Niche Processes in Evolution, Proc Natl Acad Sci USA 109 (25) 2012.
3. M. Sipos and N. Goldenfeld. Directed percolation describes lifetime and growth of turbulent puffs and slugs. Phys. Rev. E Issue 84, 035304(R) (2011).

Website last updated: January 2013