I am a PhD student in the Department of Physics
at the University of Illinois at Urbana-Champaign.
I work with Professor Nigel Goldenfeld. I am expected to graduate in May, 2024.
I am generally interested in emergent properties arising from the interplay between nonlinearity and stochasticity in complex, out-of-equlibrium systems. I am especially interested in biological neuronal systems, ecologies, and turbulence.
Education
| University of Illinois at Urbana-Champaign (UIUC)
Doctor of Philosophy in Physics Research advisor: Professor Nigel Goldenfeld Thesis: Dynamics of stochastic spatial-temporal patterns in turbulence and biological systems far from equilibrium |
Aug 2017 - May 2024 (expected) |
| Tongji University
Bachelor of Science in Applied Physics Outstanding Graduates | Sep 2013 - Jun 2017 |
Research Experience
| Traveling waves and their role in cognitive behavior in cortical neuronal networks
Research advisor: Professor Nigel Goldenfeld. Collaborator: Professor Terrence Sejnowski. |
Nov 2022 - present |
| Stochastic induced behaviors in ecological systems
Research advisor: Professor Nigel Goldenfeld. |
Jul 2022 - present |
| Statistical mechanics of transitional turbulence in wall-bounded shear flows
Research advisor: Professor Nigel Goldenfeld. Collaborator: Dr. Hong-Yan Shih. |
Oct 2018 - present |
| Interaction between blood flow, heart valves, and implanted medical devices
Research advisor: Professor Dana Grecov. Collaborator: Dr. Nick Yeh, Dr. Simon Rabkin. |
Jul 2016 - Oct 2016 |
| Statistical properties of rate events in turbulent Rayleigh-Benard convection
Research advisor: Professor Jin-Qiang Zhong. Collaborator: Dr. Hui-Min Li. |
Aug 2014 - Jul 2017 |
Publications
| 1. Jin-Qiang Zhong, Hui-Min Li, Xue-Ying Wang. Enhanced azimuthal rotation of the large-scale flow through stochastic cessations in turbulent rotating convection with large Rossby numbers. Physical Review Fluids 2, 044602 (2017). |
| 2. Xueying Wang, Hong-Yan Shih and Nigel Goldenfeld. Stochastic model for quasi-one-dimensional transitional turbulence with streamwise shear interactions. Physical Review Letters 129, 034501 (2022). |
| 3. Xueying Wang, Hong-Yan Shih and Nigel Goldenfeld. Stochastic model for energy balance and front propagation in sub-critical transitional turbulence. (Manuscript in preparation). |
| 4. Xueying Wang, Hong-Yan Shih and Nigel Goldenfeld. Critical behaviors and universality of the subcritical laminarturbulence transition in quasi-one-dimensional flows. (Manuscript in preparation). |
| 5. Xueying Wang and Nigel Goldenfeld. Demographic stochasticity gives rise to the Allee effect in predator-prey ecosystems. (Manuscript in preparation). |
Honors and Awards
| John Bardeen Award for outstanding graduate research in condensed matter physics at UIUC |
| Outstanding Bachelor Thesis Research Award of Tongji University |
| China National Scholarship |
Presentations
| Role of stochasticity in the transition to turbulence in pipe flow. APS March Meeting | Mar 2023 |
| Invited seminar at Chinese Academy of Science | Aug 2022 |
| Poster session at the Boulder Summer School for Condensed Matter Physics | Jul 2022 |
| Invited seminar at Simons Turbulence seminar series | Feb 2022 |
| Phase diagram of transitional pipe flow turbulence from a three trophic-level stochastic predator-prey model. APS March Meeting | Mar 2021 |
| Emergence of puffs, weak and strong slugs from a stochastic predator-prey model for transitional turbulence with stream-wise shear interactions. APS DFD Meeting | Nov 2020 |
Work Experience
| Research assistant | Jun 2019 - present |
| Teaching assistant of physics department at UIUC
PHYS 427 Thermal and Statistical Physics PHYS 325 Classical Mechanics I PHYS 225 Relativity and Math Applications | Aug 2017 - May 2019 |
| Summer research internship at the University of British Columbia | Jul 2016 - Sep 2016 |
| Teaching assistant of physics laboratory at Tongji University | Oct 2013 - Jul 2014 |
Outreach Experience
| Popular Science blog writer, introducing various physical phenomena to the general public |
| Volunteer at a fun, interactive physics laboratory open to the public, explaining the mechanism for each experiment |
Research
Transition to turbulence – a statistical mechanics problem in disguise
How to construct a Landau-style model for the laminar-turbulence transition?
Ref: Xueying Wang, Hong-Yan Shih, and Nigel Goldenfeld. Stochastic model for quasi-one-dimensional transitional turbulence with streamwise shear interactions. Physical Review Letters 129, 034501 (2022).
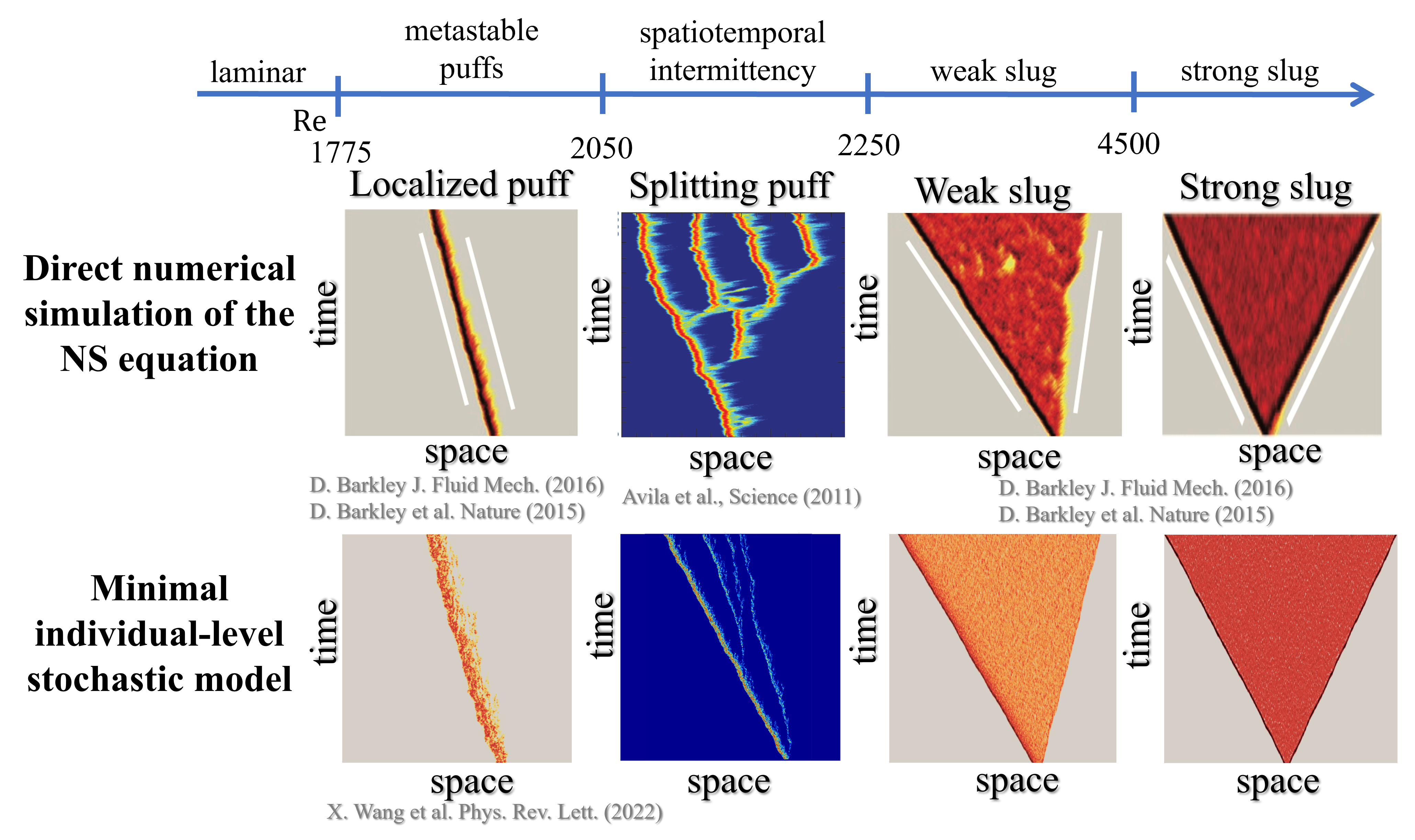
What exactly do we mean by ‘solving turbulence’? As shown in Fig 1, direct numerical simulation of the Navier-Stokes equation provides a detailed description of transitional pipe flow. Still, it does not ‘solve’ turbulence, as the mechanism that drives these behaviors is still unknown. My research employs a statistical mechanical perspective, focusing on the effective degrees of freedom that emerge from the detailed Navier-Stokes solution near the laminar-turbulence transition. This approach is analogous to how Landau theory elucidated the mechanism of equilibrium phase transition. In the context of transitional pipe flow, I chose the emergent degrees of freedom to be energy based on a numerical study of turbulent energy production and dissipation in pipe flow. I model energy balance by introducing 'nutrients' representing the mean flow kinetic energy and view the system as an ecological system with demographic stochasticity, with turbulence powered by the laminar flow. I demonstrate that the decay, splitting, and expansion of turbulence originate from different degrees of food shortages – when nutrients recover rapidly (in high-Re regime), it ensures a sufficient food source, allowing for population growth at any rate. Otherwise, the shortage of food slows down population Figure 1 Flow regimes in transitional turbulence. Top: NavierStokes equation. Bottom: My stochastic "Landau-style" modelXueying Wang – Research Statement growth, and in cases where birth rates fall below death and competition, the population will even shrink. Using these mechanisms, the model reproduces all the phases of transitional pipe flow, as shown in the second row of Fig. 1.
Why do different turbulent systems exhibit distinct transitional patterns?
Ref: Xueying Wang, Hong-Yan Shih and Nigel Goldenfeld. Critical behaviors and universality of the subcritical laminar-turbulence transition in quasi-one-dimensional flows. (Manuscript in preparation).
Our theory suggests that the laminar-turbulence transition is in the directed percolation universality class, but different flow geometries exhibit distinct patterns as a function of Reynolds number. Why? I demonstrate that, with minor modifications accounting for the differences in forcing, my model captures the transitional behavior in another system: the quasi-one-dimensional Taylor-Couette flow, depicted in Fig. 2. This enables a comparison of the critical behavior between the two systems on the same footing for the first time. By employing the exact Doi-Peliti field theory description, I showed that the leading order terms in the action of both systems converge to that of the directed percolation process near the critical point. The model also facilitates a comparison of the size of critical regions in both systems. By showing that the critical region of the Taylor-Couette flow is broader than the pipe flow, one can explain why the characteristic directed percolation pattern (like the ones in Fig. 2) is seen in the Taylor-Couette flow but not pipe flow, another long-standing open question in transitional turbulence.
Why is the statistical mechanics description of turbulence consistent with the dynamical system description?
Ref: Xueying Wang, Hong-Yan Shih, and Nigel Goldenfeld. Stochastic model for energy balance and front propagation in sub-critical transitional turbulence. (Manuscript in preparation).
The conceptual picture behind the laminar-turbulence transition is quite subtle. On the one hand, turbulence is a deterministic phenomenon, and its subcritical bifurcation is considered the counterpart of first-order phase transition. On the other hand, directed percolation is a stochastic process undergoing a continuous phase transition. The intangible tension between subcritical bifurcation and directed percolation transition has never been concretely studied. In my work, I showed that the deterministic limit of both the model and the directed percolation process produces ‘pulled waves’ that describe a stable (turbulent) state invading the unstable (laminar) one. At first glance, this seems in direct conflict with the properties of subcritical bifurcation, which exhibits bistability. This problem is solved by demographic stochasticity – it introduces an effective singular perturbation to the pulled wave dynamics, modifying them to bridge two stable states. Moreover, this ‘modified pulled wave’ is in the same universality class as the original pulled wave. By tackling this specific problem, I was able to address this previously ambiguous paradox directly.
Finished and ongoing work in ecology
Can the ecological Allee effect come from pure demographic stochasticity?
Ref: Xueying Wang and Nigel Goldenfeld. Demographic stochasticity gives rise to the Allee effect in predator-prey ecosystems. (Manuscript in preparation).
In my turbulence model, I highlighted the limiting effect of nutrient density ρ on organism growth. Specifically, when the nutrient population density ρ is small, it can slow down the growth of active organisms, even leading to a decline in the organism population if its growth rate becomes smaller than the decay rate. In the turbulence model, the nutrient density is the mean flow kinetic energy. Similar phenomena can be observed in many reallife, stochastic ecological systems where the growth of one organism depends on the population density of another. This phenomenon can be exemplified by an individual-level model of predator-prey dynamics, where a decline in prey density is always followed by a decrease in predator density of the same scale, resulting in a persistent oscillation, i.e., the quasi-cycle. While these dynamics may seem intuitive and straightforward, their origins are deeply rooted in the subtleties of demographic stochasticity.
In my work, I discovered that all ‘nutrient-limiting effects’ are lost in the deterministic approximation, indicating a stochastic origin of such effect. By analyzing its first-order approximation, the Langevin equation, a negative Ito drift emerges in the growth rate. This term is inversely proportional to the square root of ρ, indicating that its magnitude amplifies as the population diminishes. Such a phenomenon becomes dominant at low population densities ρ, leading to a decreasing population growth rate as ρ decreases. This behavior is similar to the phenomenon known as the Allee effect well-documented in ecology. The Allee effect describes a scenario where the growth rate of a population decreases at lower population densities ρ, characterized by a distinct curvature change in the growth rate function with respect to ρ. While the Allee effect is typically introduced via a nonlinear deterministic term, my findings indicate that the appearance of a similar effect can arise simply from the stochastic nature of ecological systems, without the need for any additional mechanistic explanations. A detailed and spatially-resolved explanation of this effect can be achieved through a field-theoretic analysis.
Ongoing work in neuroscience
Unlike their artificial analogs, biological networks exhibit spiking dynamics and transmission time delays. While these features add to the complexity of their dynamics, they significantly enhance the potential capabilities of the network. For instance, spiking dynamics enables the neurons to engage in temporally precise communication; it also allows the network to have “self-tuning” abilities through mechanisms such as spike-timing-dependent plasticity, etc. Such features underscore the innate ability of biological neuronal networks to self-organize. My research seeks to understand how emergent computational and cognitive functions arise in biological neuronal networks.
Dynamics of large-scale circulation in turbulent rotating Rayleigh-Bénard convection
In my undergraduate years, I worked on large-scale circulation dynamics in turbulent rotating Rayleigh-Bénard convection. My collaborators built the Rayleigh-Bénard convection cell on a slowly rotating plane and operated it in the parameter regime where the large-scale circulation shows up. They measured how the average azimuthal rotating speed of the large-scale circulation plane changes with the Rossby number. In the large Rossby number region, they discovered an unexpected growth of the relative retrograde azimuthal rotating speed of circulation plane with increasing Rossby number. Existing theories could not explain this phenomenon.
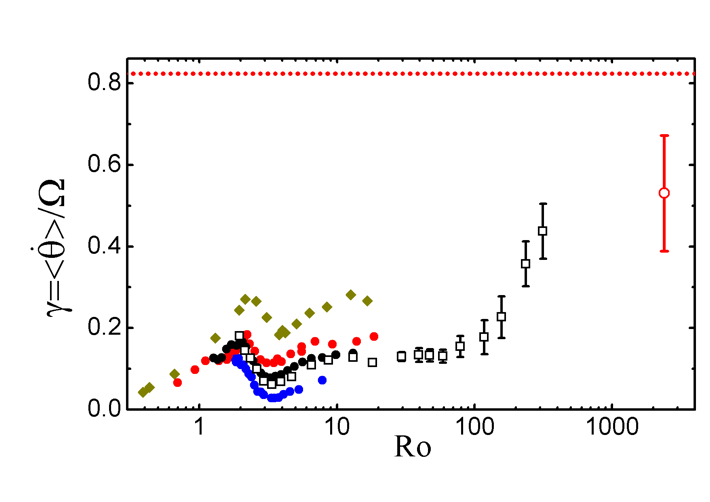
From the experimental data, we found out that the growth of relative retrograde rotation speed is caused by rare stochastic events like cessation and reversal of the circulation plane that are neglected by existing theories. During these rare events, the circulation plane rotates much faster than usual.
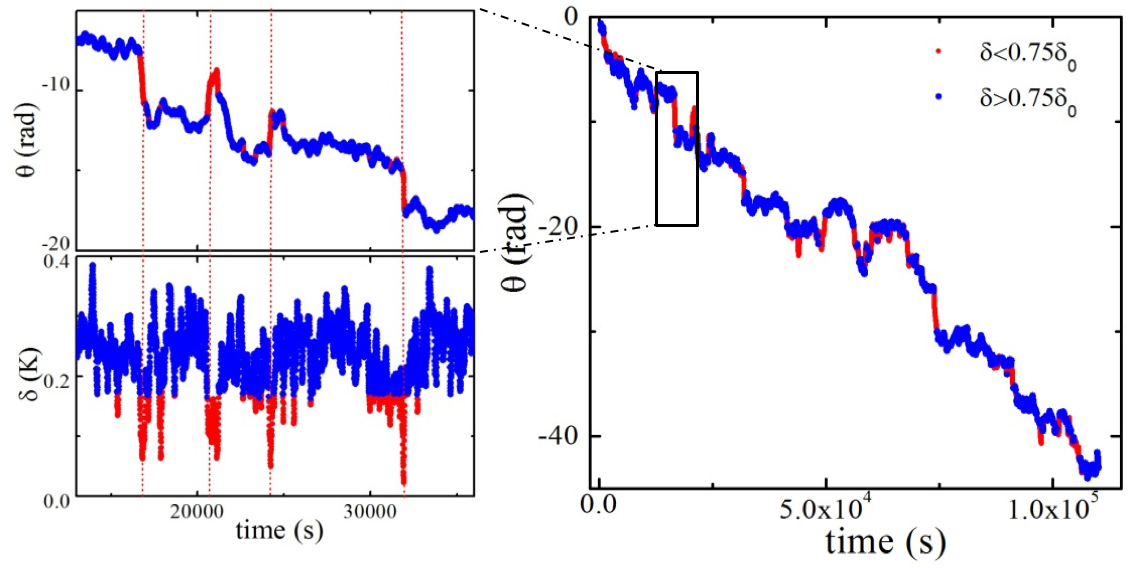
To quantitatively check how much the rare events contribute to the abnormal growth, we started from the idea of an early model and a revised theory based on it, where the system is described by two Langevin equations with additive white noise that captures the dynamics of the azimuthal angular motion and the strength of the circulation plane.
By decoupling the linear rotating component, we were able to reduce the model to an Ornstein-Uhlenbeck process-like form and further estimate theoretical values of frequencies of rare events and average azimuthal displacement per event at different Rossby number region. Based on these values, we calculated theoretically how much the rare events contribute to total relative rotation speed, which agrees very well with experimental values. Thus, our conjecture was confirmed, and the abnormal increase of rotation speed was explained -- the behavior of the large-scale circulation during those stochastic rare events are indeed the major cause of the unexpected growth in retrograde relative plain rotation speed.

We also estimated correction to previous models from Reynolds stress by fitting the probability distribution functions of plane rotation speed and circulation strength.
I did part of the theory and most of the data analysis for this project.
