Research
Research Overview
My research uses computational and analytic techniques from statistical physics to examine spatial patterns and dynamics in complex biological systems.
In collaboration with experimentalists at MIT and UIUC I have shown how noise can stabilize emergent behaviors such as Turing patterns in biofilms. Normally one would think that noise destroys patterns but we found that fluctuations in the copy number of signaling molecules acting as activator and inhibitors of gene expression leads to pattern formation. Surprisingly we can show theoretically that these fluctuations increase the range of experimental conditions in which patterns can form.
In collaboration with experimentalists at UIUC, we have observed how evolution acts on variation in time, space, and genome locus by imaging live cells with fluorescent reporters that allow us to track transposons dynamics. Transposons, also known as jumping genes, are found in all organisms and have activity that can cause mutations and drive evolution. As part of this collaboration I developed the software for image analysis of the cells and analyzed the resulting statistics of events. We discovered that the excision rate of transposons depends on orientation of the element, spatial location of the cell, and some heritable factors.
In a follow-up experiment, I recently developed a model to explain our collaborators' observation that the number of retrotransposon transcripts, transcripts produced by a copy and paste type of mobile genetic element, produces an exponential growth dependence defect. I developed a model for the copy number dynamics of retro-elements and the time it takes these elements to be lost from a population of cells depending on the observed growth rate defect, transposition rate, and inactivation rate. This model explains why Group II introns are present in about 30% of bacterial species, while retrotransposons are essentially absent. This research sheds light on the early evolution of the eukaryotic spliceosome, the cellular machinery allowing complex organisms to remove intra-gene junk DNA during gene expression.
Download a copy of this research statement here
Stochastic Turing Patterns
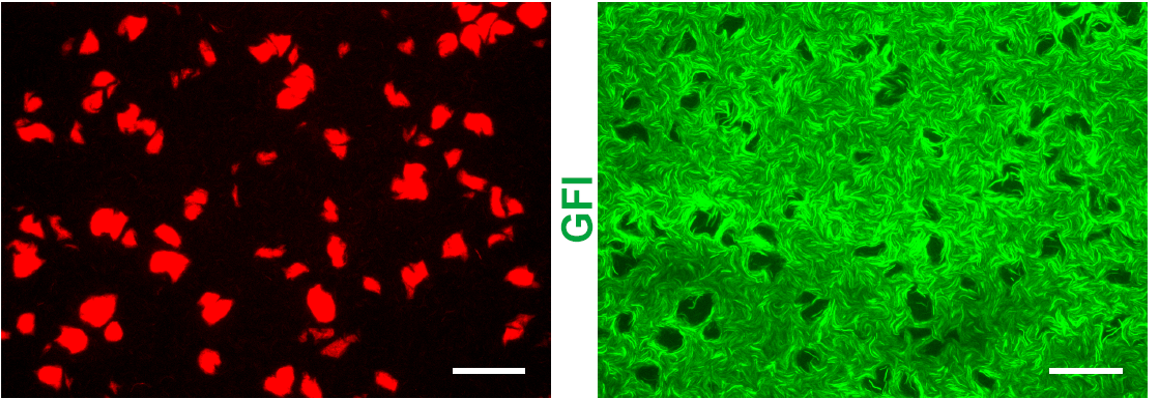
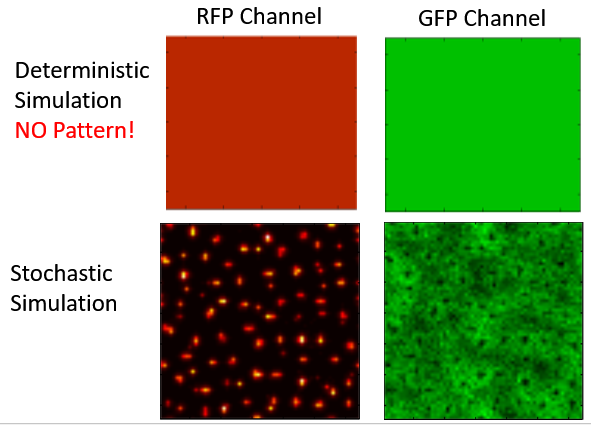
In Turing's 1952 paper, "The Chemical Basis of Morphogenesis," Turing showed how a periodic pattern instability can emerge from an initially uniform activator inhibitor reaction diffusion system. . In this picture the activator activates its own production and that of the inhibitor while the inhibitor inhibits its own production and that of the activator. In an initially homogeneous state the activator will amplify any small perturbation creating more activator and inhibitor locally. The inhibitor then diffuses more quickly than the activator suppressing further growth. In this way a periodic pattern will form. Note that in the traditional analysis this requires the two morphogens to have very different diffusion rates for pattern formation. On the other hand, in a stochastic model using the intrinsic noise from the birth and death processes, it turns out that the diffusion rates do not need to be so widely different.
I analyzed the data from an experiment that was conducted at MIT where our collaborators attempted to engineer a Turing pattern. From my analysis I was able to show that the patterns they formed were actually stochastic Turing patterns rather than traditional Turing patterns. I did this by measuring the power spectrum of the pattern and showed it was consistent with theoretical predictions for the power spectrum of a stochastic Turing pattern. In addition, I analyzed and simulated a detailed model of their system and showed for the measured parameters of their system the model can only produce patterns if the stochasticity of the birth and death processes were included. I also mapped how much of parameter space would produce stochastic patterns as compared to deterministic Turing patterns.
Transposable Elements
Transposable elements(TE), more colloquially known as jumping genes, are DNA sequences that can move their position around the genome. There are two main types of transposable elements, DNA transposons which use a cut and paste mechanism of transposition and retro-transposons which use a copy and paste mechanism of transposition. Transposable elements make up a large fraction of eukaryotic genomes. For example, roughly 85% of maize's genome is TE and 46% of the human genome consists of TE. Transposable elements through their activity generate mutations in the genome and thus are important for understanding disease, development, and evolution.
Transposons

Little is known about the dynamics of TE elements in live cells. Previous works inferred transposition rates from bulk sampling of cells which averages over many cells and loses information about fluctuations. Others attempted to measure the rates from phylogenetic comparisons which suffers from the limitation that only events that have become fixed in a population can be observed. This misses events that could cause extinctions and the corresponding estimates of rates will likely underestimate the rate of transposition. To overcome these limitations our experimental collaborators use a transposon to interrupt a promotor for the expression of mCerulean. When the transposon excises it will produce a full promotor and the cell will start to express mCerulean and glow blue. Additionally the protein that is responsible for excision of the transposon in tagged with another fluorescing protein that glows yellow.
By observing the fluorescence of cells the amount transposase can be quantified and it is possible to determine if a transposition event has occurred. I developed an image analysis software to automatically detect when and where transposition had occurred. Using this software we were able to extract rates of excision of 6.3e-3 events/cell/hr. Furthermore we were able to test if excision was uniform in time and space. We found the rate of transposition to be growth state dependent. Initially no events were detected until growth arrest. Events were uniform in time upon their initiation in growth arrest for 35 hours and had Poisson statistics. Furthermore we found excision events to be clustered in space as shown by an excess in the radial correlation function within a few cell lengths as compared to simulations of completely uniform event distribution. This clustering of excision events suggests that there may be a heritable change that effects excision rate. To test this hypothesis we measured the distribution of event rates from 984 colonies. We found that the resulting distribution was well fit by a twostep process: first a heritable change can occur during exponential growth that predisposes cells to TE activity; then upon growth arrest the cells containing this change have a probability of their TEs excising.
The growth state dependence, spatial clustering, and heritability of TE excision suggests that mutations caused from reintegration will also be heterogeneous and growth state dependent. This is important since many models of mutation and evolution start with the assumptions of uniform and homogenous mutation rate.
Retrotransposons
Retrotransposons are abundant in Eukaryotes but are rare in bacteria. In Eukaryotes retroelements exist in high copy number while in bacteria, a simpler form of retroelement known as a group II introns can be present, but only in low copy number and only in 30% of bacterial species. In humans the retrotansposon LINE-1 (L1) makes up 17% of the human genome, with about 500,000 integrants and roughly 100 active copies, whereas group II introns in bacteria typically have only 1-10 copies.
To try to characterize some of the differences between bacteria group II introns and Eukaryotic retro-transposons our experimental collaborators succeeded in transplanting a human L1 into a bacterial host (E. coli). They observed that L1 expression is detrimental to the growth of E. coli and B. subtilis. The growth rate of these bacteria was exponentially depressed with additional copies of L1 transcript. I modeled this by a simple binary growth model where each transcript has a certain probability of integrating and disrupting the cell’s ability to grow. Thus the probability that a cell will be able to grow is the binomial distribution with zero negative integration events. This simple model produces an exponential growth defect. Our experimental collaborators measured the growth defect for both bacteria and measured the growth defect for group II introns.
I also developed a model for the copy number of retro-elements given a measured birth defect, transposition rate per transposon, inactivation rate of the retro-elements, and death rate of bacteria. This more complicated model predicts that the measured growth defect of L1 in bacteria will cause the bacteria to quickly lose L1, matching results of experiment. It also predicts that for the measured growth defect of group II introns, they will persist in low copy numbers for at least millions of generations, consistent with the observations of group II introns in bacteria. Finally it predicts that for L1 to persist in human populations at high copy number the growth defect must be very small. This may be achieved in Eukaryotes by the spliceosome which limits genetic damage caused by integrants.
In summary, this project suggests that the spliceosome in Eukaryotes may have evolved in response to selection pressure from retroelements. In particular it is consistent with phylogenetic evidence that shows how group II intron proteins were early predecessors of eukaryotic spliceosomal proteins, suggesting that the spliceosome was transmitted to Eukaryotes by an early horizontal gene transfer from Bacteria.
Image Analysis of Maize Roots
Andrew Leakey in the Plant Biology department runs the Free Air Concentration Enrichment (FACE) experiments, in an attempt to see how global climate change will affect plant yields. In this experiment CO2 is pumped over a field. In one of the experiments he wants to know the phenotypic changes to the root system. Images are taken from micro-rhizotrons, fiber optic cameras inserted in pipes near the root system of interest. The resulting photos are very dirty and contain many challenges to traditional segmentation, including many variations in lighting, obstruction due to moisture on the tube, cracks in the soil, and different morphologies of the root systems. Hundreds of thousands of images are captured from these micro-rhizotrons. Previous to my involvement these images were being segmented by hand.
When I first started on this project I developed an ad hoc technique to segment the images using various ideas such as modeling a background for background subtraction, looking at patterns of edges indicating a root, and looking at the Fourier spectrum of parts of the image. While these techniques were sufficient to identify certain classes of the roots they were not able to identify all roots and failed on very dirty images.
Together with an undergraduate that I mentored we used machine learning techniques to automatically quantify and identify Maize roots. We used a convolutional neural networks to determine the amount of roots in an image. We trained our neural network using images that had been segmented by hand in previous seasons. This new technique resulted in an accuracy almost equivalent to that of human experts.