Farshid Jafarpour

Dynamics of Age Distribution in Populations of Asymmetrically Dividing Bacteria

Bacterial cells are known to grow exponentially in number when they are kept in constant favorable conditions for a long time. Under such conditions (also known as balanced growth), the fraction of cells at each given age (the age distribution) becomes stationary. In this project, I have found an exact analytical solution for the dynamics of age distribution and population growth rate of Caulobacter Crescentus, a model organism for asymmetric cell division, as a functional of experimentally measured inter-division time distribution of single cells, before and during balanced growth. A population of C. Crescentus consists of two phenotypes of cells: a stalked phenotype that attaches to surfaces through an adhesive stalk, and a flagellate swarmer phenotype. Stalked cells grow and divide into two daughter cells of each phenotype. The stalked daughter stays attached, while the swarmer daughter swims away until it differentiates to a stalked cell, attaches to a surface, and starts its chromosome replication and division process.

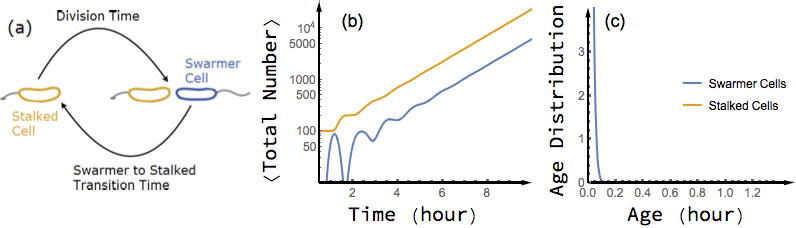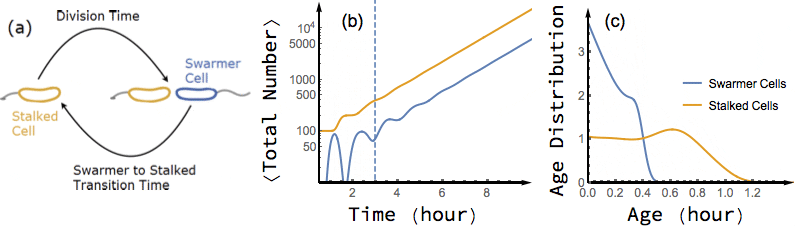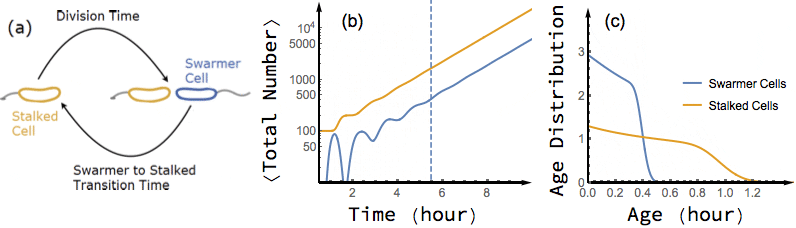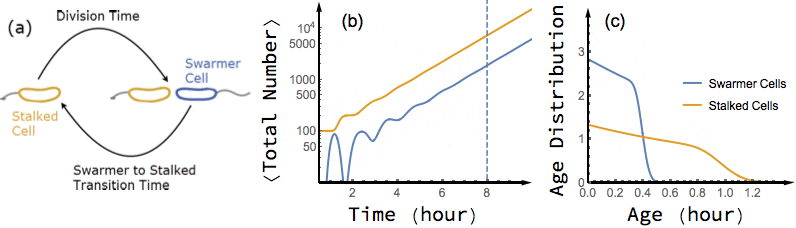
While the inter-division time distribution of stalked cells can be measured in single cell experiments, the swarmer to stalked transition time has not been directly measured. However, our analytical results on the dependence of growth rate on swarmer to stalked transition time, along with the experimentally measured inter-division time distribution, provides a method to estimate this time scale. Additionally, we predict a transient oscillation in the number of each phenotype in a population starting far from balanced growth. In particular, I have shown that if we experimentally measure the growth rate of a population of initially synchronized cells over time, we can infer both inter-division time distribution and swarmer to stalked transition time distribution from the observed oscillations.

Related Publication:

• F. Jafarpour, C. S. Wright, H. Gudjonson, J. Riebling, E. Dawson, K. Lo, A. Fiebig, S. Crosson, A. R. Dinner, S. Iyer-Biswas. Bridging the time scales of single-cell and population dynamics. Phys. Rev. X 8, 021007 (2018). (PDF). https://doi.org/10.1103/PhysRevX.8.021007
• Physics Synopsis: Connecting Noisy Single-Cell Dynamics to Smooth Population Growth. (link)

Origin of Life: Evolving Dynamical Systems

I am interested to answer the following question: What were the conditions on the earth around four billion years ago that led to a dynamical phase transition between the inanimate matter and the first forms of life? More generally, I am interested to know what are the general set of conditions required for a dynamical system to undergo a transition of this sort. To answer these questions, I am designing an ecosystem of coevolving computer meta-programs that modify each other. I use the mathematical techniques in recursion theory to analyze different dynamical regimes of such ecosystems.

Giant Amplification in Stochastic Turing Patterns

Turing patterns are nonequilibrium spatial instabilities that arise in activator inhibitor systems when the activator diffuses sufficiently slower than the inhibitor. They were believed to be responsible for a wide range of pattern formations and spatial inhomogeneities observed in biological systems. However, the mathematical requirement for the vast separation of the two diffusion constants presents a difficulty to confirm that the observed patterns are Turing patterns. In systems in which the ratio of the two diffusion constants is just under the required value for the formation of a Turing pattern, the homogeneous solution can be destabilized by noise (either intrinsic or extrinsic) leading to similar patterns known as stochastic Turing patterns. In other words, the presence of noise expands the range of parameters for which a steady state spatial pattern can be observed in a system, making the experimental realization of these pattern significantly easier. The mechanism for the stochastic Turing patterns can be understood through the following observation: Outside of the range of the parameters for classical Turing patterns, all the eigenvalues of the linear stability operator are negative, but their value depends on the wave number $k$ in Fourier space. In the presence of noise, the Fourier modes corresponding to the most negative eigenvalues decay quickly, while the slower modes drift away under the influence of the noise giving rise to patterns with well-defined length scales.

The amplitude of stochastic Turing patterns can be estimated to be equal to the variance of the noise multiplied by the decay time scale of the slowest Fourier mode. This presents another challenge for the experimental observation of these patterns when the amplitude of the noise is small. However, we have shown that the steady state amplitude of stochastic Turing patterns can be drastically amplified by the transient dynamics if the linear stability operator is far from Hermitian. This behavior can be understood through the following two observations: 1) When the linear stability operator is far from Hermitian with negative eigenvalues, even though all the eigencomponents of the state vector decay exponentially with time, the norm of the state vector can temporarily grow. 2) The presence of noise can keep the system in the transient regime of the deterministic dynamics. This unexpected amplification makes the stochastic Turing patterns a more promising candidate to explain the experimentally observed patterns.

In this project, I have proposed a natural measure for nonnormality of an operator and have characterized the amplification of the stochastic Turing patterns as a function of the nonnormality of the linear stability operator.

Related Publication:

• Tommaso Biancalani*, Farshid Jafarpour*, Nigel Goldenfeld. Giant amplification of noise in fluctuation-induced pattern formation. Phys. Rev. Lett. 118, 018101 (5 pages) (2017). (PDF). https://doi.org/10.1103/PhysRevLett.118.018101

Homochirality and Noise Induced Bistability

In organic chemistry, molecules that are not superimposable on their mirror image are called chiral. Many of biological molecules such as sugars and amino acids are chiral, and their chirality plays an important role in structure and function of macromolecules that are built from them in living cells. It is remarkable that despite the diversity of such macromolecules in different living organisms, all of amino acids found in biological systems are $L$-chiral (left-handed) and all of the sugars are $D$-chiral (right-handed). The origin of the homochirality of sugars and amino acids in biology is not well understood.

In 1953, Charles Frank suggested that homochirality is a consequence of autocatalysis. To show this, he constructed a simple model in which $L$ and $D$ form of a chiral molecule are autocatalytically produced from an achiral molecule $A$, and they are consumed by reacting with each other. The latter reaction that has no biological justification is called chiral inhibition. By solving the rate equations for these reactions, Frank showed that there are three fixed points in the dynamics of this system: a fixed point at the racemic state ($50$% $D$ - $50$% $L$) which is unstable and two homochiral states that are stable. However, the existence of these fixed points is dependent on the chiral inhibition mechanism. By removing the chiral inhibition reaction, we lose the stability of the homochiral states. Moreover, the addition of even the slightest amount of non-autocatalytic production of $L$ and $D$ makes the racemic state the global attractor of the system.

In the absent of chiral inhibition, even with a small amount of non-autocatalytic production where the racemic state is the global attractor of the deterministic model, I have shown that homochirality can arise due to the stochastic nature of chemical reactions. In this model, the homochiral states are not fixed points, but when the autocatalysis is the dominant production mechanism, the functional form of the stochasticity of autocatalytic reactions stabilize the homochiral states.

Intuitively, autocatalysis in average, produces a proportionate amount of $L$ and $D$ molecules to the initial condition, leaving the chirality of the system unchanged at the deterministic limit. However, chemical reactions are stochastic, and every time an autocatalysis reaction happens, the chirality of the system changes by a small discrete amount. These zero mean random fluctuations that are caused by the stochasticity of the chemical reaction cause the chirality of the system to slowly drift away from the racemic state. However, the stochastic effect of the autocatalytic reactions is zero at the homochiral states (the autocatalysis produces more of the same chiral molecules that exist in the solution leaving the chirality of the system unchanged), while it is maximum at the racemic state. Therefore, the chirality of the system drifts away from the racemic state and gets trapped in one of the homochiral states.

Additionally, I have shown that when autocatalysis is dominant, coupling many well-mixed system of chemical reactions through diffusion results in synchronization of the homochiral states of all of the systems, indicating that the spatial extension of this model exhibits stable global homochirality

Related Publications:

• Farshid Jafarpour, Tommaso Biancalani and Nigel Goldenfeld. Noise-induced mechanism for Biological Homochirality of Early Life Self-Replicators. Phys. Rev. Lett. 115, 158101 (5 pages) (2015). (PDF) https://doi.org/10.1103/PhysRevLett.115.158101
• Farshid Jafarpour, Tommaso Biancalani, Nigel Goldenfeld. Noise-induced symmetry breaking far from equilibrium and the emergence of biological homochirality. Phys. Rev. E 95, 032407 (18 pages) (2017). (PDF) https://doi.org/10.1103 /PhysRevE.95.032407

Velocity Statistics of Dislocations in Plastic Flow

Plastic deformation of crystalline material under stress is known to be a smooth process in macroscopic scales. However, it has been shown that in smaller scales, the deformation of these material is not a smooth function of applied stress. In these systems, topological defects, such as dislocations, have a slowly evolving configurations with rapid collective rearrangements. These collective rearrangements are responsible for the intermittent character of the deformation (see figure below). Discrete dislocation dynamic simulations have shown a power-law scalings for the probability density function of velocity of the dislocations. The self similar characteristics of the velocity distribution is often attributed to the collective interaction of dislocations that leads to the intermittent dynamics, but the mathematical connection between these power laws and the intermittency of the deformation has not been established.

We have worked out the probability distribution of velocities of dislocations using methods from stochastic calculus by mapping the problem of motion of dislocations to Dyson's model of two dimensional electron gas confined to one dimension. Dyson's model was originally developed to calculate the statistical properties of energy levels of heavy nuclei. We have shown that the power-law distribution of velocities of dislocations is not a signature of collective dynamics. However, the deviation of the exponent of this power law from the exponent expected in the absence of collective dynamics can be used as a measure of collective interactions.

Related Publications:

• Farshid Jafarpour, Luiza Angheluta, and Nigel Goldenfeld. Velocity statistics for interacting edge dislocations in one dimension from Dyson’s Coulomb gas model. Phys. Rev. E 88, 042123 (8 pages) (2013). (PDF) https://doi.org/10.1103/PhysRevE.88.042123